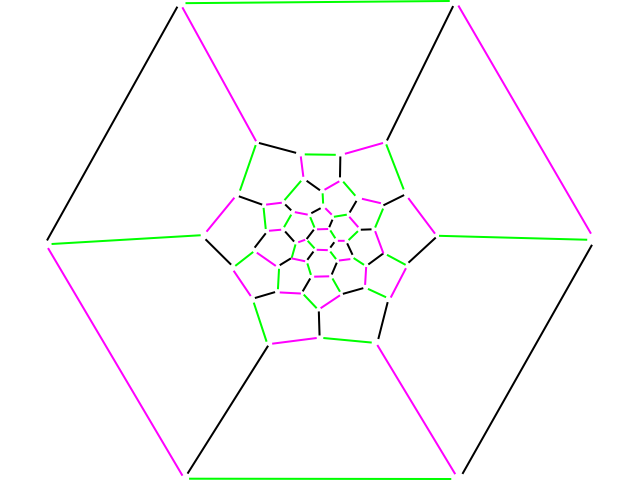
Today someone asked whether you could colour a truncated icosahedron with 3 colours only, such that no two adjacent edges had the same colour.
After some research I found that it was possible, and that one way of finding such a colouring is as follows:
1. Draw the corresponding graph.
2. Find a Hamiltonian circuit in that graph. [Got this from Tom Hull's submission to Origami 3]
3. Colour the Hamiltonian circuit with two colours, alternating between them as you go along the path.
4. Give the remaining edges the third colour.
This picture shows the result I got. It's by no means the only colouring that is possible, but the colours are relatively evenly distributed on it. That is, every pentagon and hexagon has at least one module of each of the 3 colours. This might be interesting to those of you out there that do lots of modular origami.

Comments
Submitted by Anonymous (not verified) on 24 September 2009 - 2:10am Permalink
Interesting.
I read that wikipedia page all the way through, and understood 40% of it, enough to know what you are talking about, and the concept.
WOW!!!!!!
Submitted by Elvis D. (not verified) on 1 January 2011 - 4:01am Permalink
our of curiostity does this
our of curiostity does this show all pieces(all 90)
Submitted by Sara on 2 January 2011 - 1:31pm Permalink
Sure!
Yes, it does.
Submitted by Kazza the Blank One (not verified) on 12 April 2011 - 2:18pm Permalink
Path doesn't join?
I was just staring at this and I think there might be a mistake .. I think the Hamiltonian path is meant to be one continuous line? It looks like you have two separate paths there?
Submitted by Sara on 17 April 2011 - 9:47am Permalink
Ah, read carefully
Ah, read carefully:
1. Draw the corresponding graph.
2. Find a Hamiltonian circuit in that graph. [Got this from Tom Hull's submission to Origami 3]
3. Colour the Hamiltonian circuit with two colours, alternating between them as you go along the path.
4. Give the remaining edges the third colour.
This says that once you have a Hamiltonian circuit, you'll indeed chunk it up and color it with two different colors. :)
-- Sara
Submitted by Kazza the Blank One (not verified) on 17 April 2011 - 2:10pm Permalink
Looks better now!
Looks fixed now :)
I made a large phizz buckyball with seven hexagons on each of the "faces" between the pentagons. The hamiltonian path on it surprised me, but I'm yet to figure out how to show it nicely (and I don't fancy drawing a diagram like the one above with all 270 edges! heh)
http://kazza.id.au/2...
Submitted by Janine (not verified) on 26 September 2020 - 2:44pm Permalink
Thanks!
I made one and it worked! I had drawn the diagram with the pentagon in the middle but I couldn't get the colours to work out. I followed yours and my 90 sonobe units are now a soccer ball :-)
Add new comment